Learning to Calculate Interquartile Range
Interquartile is one of the most significant elements of mathematics. It is indeed the measure that either the middle fifty exists in the data or not. It is of extreme value due to its fabulous applications. For instance, it helps in the determination of SAT scores or school performance. A quartile calculator is a digital approach that intent to calculate the IQR statistics for the given observations.
Significance of Interquartile Range:
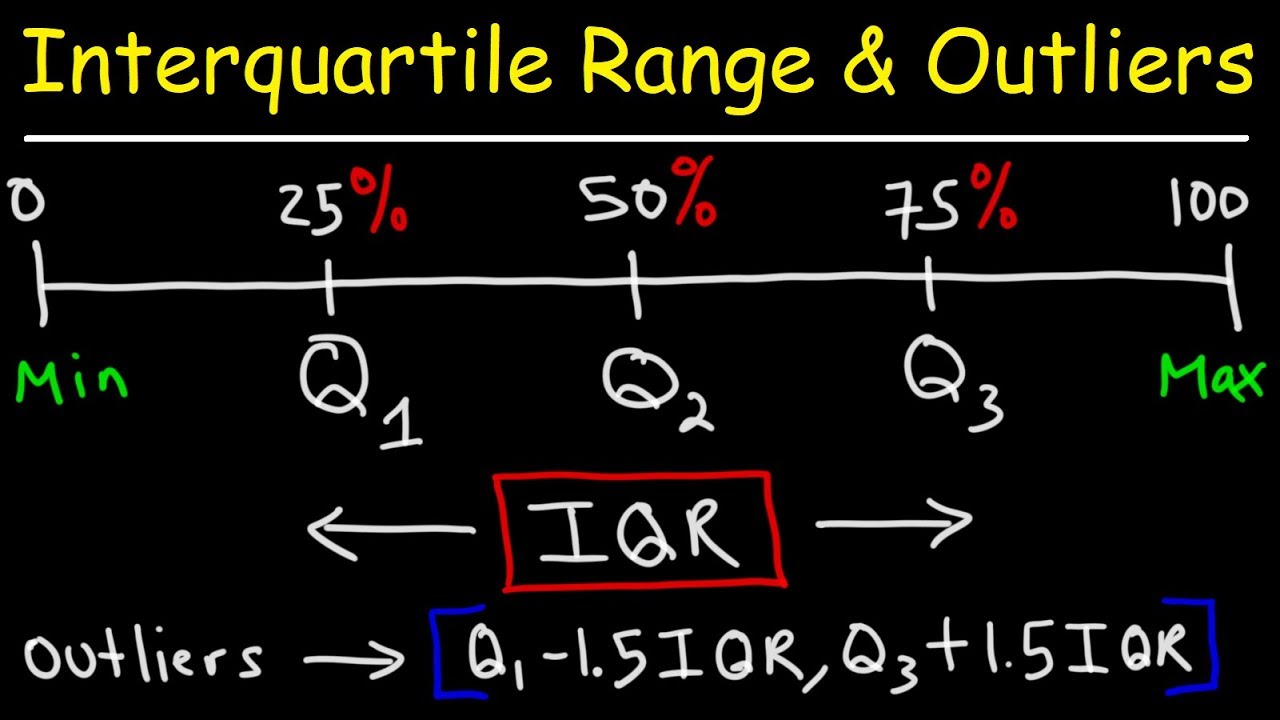
Interquartile range helps in the determination of either the value is an outlier or not. Moreover, it also helps to address the identification of outlier strength, either strong or weak. A low quartile is a reliable approach that provides limitless calculations without any charge. Besides the interquartile calculator, there is another approach for the calculation of the interquartile range. Users can find IQR in Excel easily by applying function to differentiate both high and low values. When it comes to the measure of central tendency, then IQR proves to be a valuable approach. It is because it defines the extreme values of the data set and divides it into four sections. Quartile deviation can be found by dividing the difference of quartile by 2. It includes the difference of both upper and lower quartiles, which is then divided into half. It is also known as semi-interquartile. The formula for this is given as:
Q.D = (Q3 – Q1) / 2
The difference between both the quartile of lower and upper value is known as the interquartile range. It is indicative of the spread of the middle value of the given data set. The interquartile range is a valuable approach in calculating box width in the Box and Whisker plot. In the quartile calculator, you can mention the data set either with space or commas. Indeed, you also get the golden opportunity to define it in your desired manner.
Quartile Formula:
The quartiles calculator makes a calculation on the values or data set with the use of the IQR formula. IQR formula responsible for the calculations are given as:
IQR = Q3 –Q1
Here, Q3 represents the third quartile while Q1 is the first quartile. Q1 represents the 25th percentile, while Q3 represents the 75th percentile. Interquartile calculator demands the data set for processing the outcome. The interquartile range cannot be clearly visualized with box plots but helps in the determination of IQR. The third quartile calculator helps in the determination of IQR through Box plot assistance.
How to Find Quartiles?
Quartile calculator is one of the most splendid online calculators which helps to find quartile. Gather the data for the observations or research and mention the data set in the online calculator’s empty field. Ensure to mention the values or data in it in ascending order. For instance, if the data set is 19, 18, 27, 2, 1, 3, 15, 13, 5, 6, and 7. You need to enter it in the upper quartile calculator as given below:
1,2,3,5,6,7,13,15,18,19,27
The next step is to determine the value of the median for the data set. When you mention the values in random order, then the median cannot figure out correctly. After doing so, find out the upper and lower quartile. Now, add parentheses to the data set below and above the median. For the given data set, it is given as:
(1,2,3,5,6),7,(13,15,18,19,27)
For the data set, Q1 and Q3 are indicative of the lower part for the median and upper part for the median, respectively. Here, the value for Q3 is 18, while the value for Q1 is 3. The interquartile calculator is super easy to use and provides instant results. Now, enter the upper and lower median values in the quartile formula for determining the outcomes.
IQR = 18 – 3
IQR = 15






